Statistical physics of signal propagation in deep neural networks
Here I’ve summarized some of the main ideas that underlie the theory of signal propagation in deep neural networks. This theory, which is strongly inspired by the physics of statistical field theory, explains the success of ReLU as an activation function for deep networks and also predicts that the Kaiming initialization scheme is optimal. I wrote this as a final report for a course on critical phenomena in equilibrium and nonequilibrium systems. I hope it’s informative!
Introduction
In machine learning, we are interested in learning patterns in data. In regression problems, we focus on learning a function that uses data (e.g. a digital image) to predict properties of the data (e.g. whether the image contains a cat). To do this, we use a general-purpose function approximator: a neural network. A neural network (NN) parameterizes a family of functions by stacking layers of interleaved affine transformations and element-wise nonlinear transformations. For example,
where
Unfortunately, we lack a complete theory that predicts the final performance of a given NN before actually training it. The fundamental difficulty is that neural networks may have billions of parameters whose training dynamics are coupled. This justifies using tools from statistical physics to uncover the basic behaviors and properties of these large-scale systems. In fact, mean field theory, partition functions, replica calculations, phase transitions, and more have become standard in NN theory, reflecting a long history of contributions from statistical physicists to NN theory (Bahri et al. 2020).
In the past decade, practitioners have provided evidence that deeper neural networks a) perform better, but b) are more challenging to optimize. Subsequent work empirically found that a particular choice of
Field theory of neural networks
In a trained neural network, we expect that two input vectors that are semantically similar (e.g. that both are images of cats) should be pushed towards each other as the input propagates through the network. In this sense, the role of a neural network is to extract semantic structure from the relevant data, which is typically some complicated submanifold in input space (i.e. a ‘typical’ random vector in image space is just noise; we only care about the manifold of ‘natural’ images).
Of course, the way an input is transformed through the network depends on the affine parameters. While the optimization algorithm provides the dynamical equation for the parameters, we must also specify the initial conditions. In practice, affine parameters are initialized i.i.d. Gaussian as
where
where
Note that
However, a major challenge remains. Although the first-layer “field”
This field-theoretic framework allows us to theoretically compute the correlator for a variety of choices of
Criticality analysis
For a NN to be initialized at criticality, we need the correlator to approach a nontrivial fixed point
where the expectation is tractable in the mean-field limit since it depends only on
Roberts, Yaida, and Hanin (2022) use perturbative techniques to compute the fixed point
which has a fixed point at
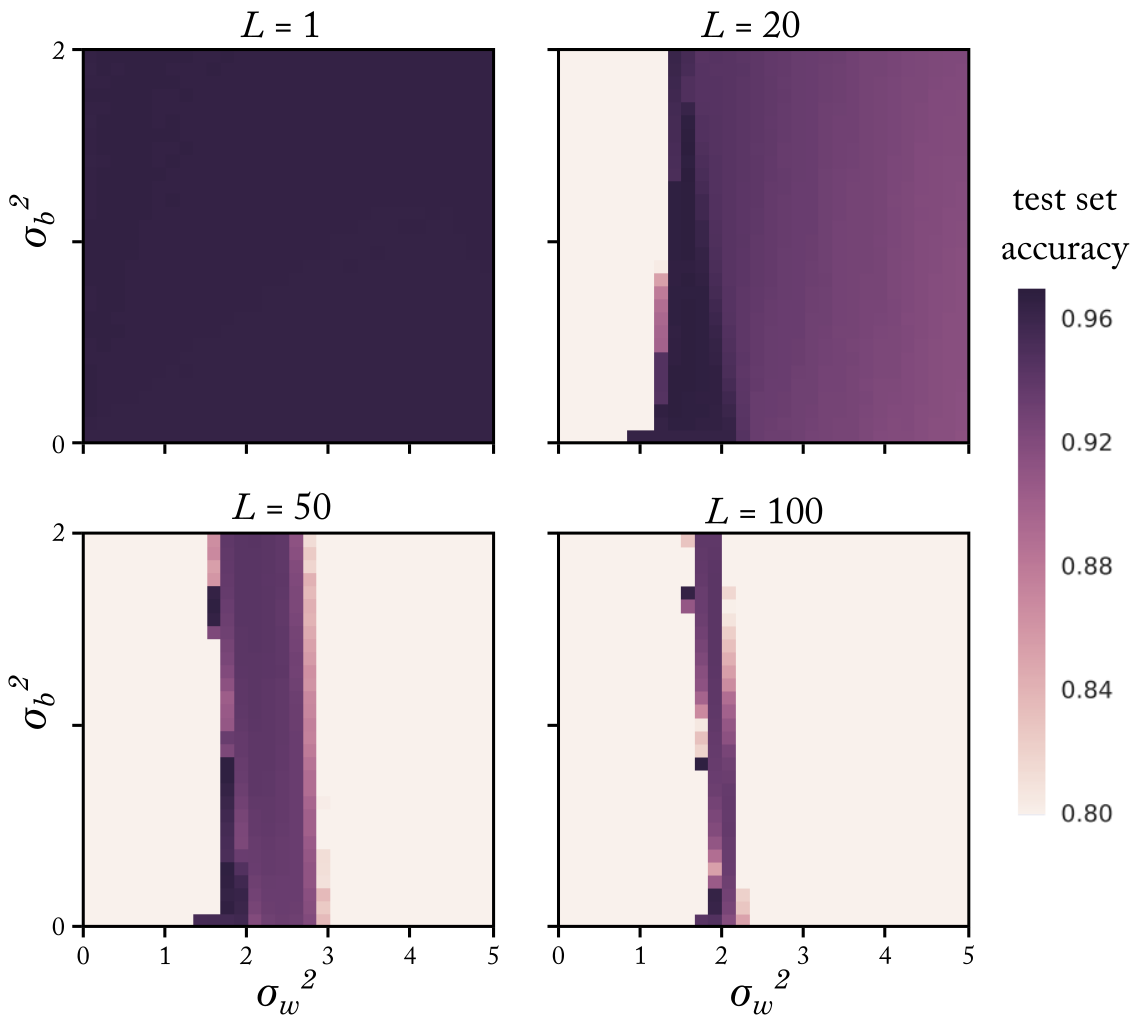
We can use this formalism to repeat this calculation for other choices of nonlinearity
Future directions
Do NNs far from the mean-field limit behave qualitatively differently? Can the field theory framework handle task-specific NN architectures where the affine transforms may have additional structure? Can we go beyond initialization and make quantitative, data-dependent predictions about training dynamics? The field theory formalism presented here is one of many frameworks used to approach the slew of open questions remaining in NN theory. Rapid engineering improvements only deepen the gap between theory and practice; it will take a coherent synthesis of varying perspectives to develop a complete theory of deep learning.
References
- Bahri, Yasaman et al. (2020). “Statistical mechanics of deep learning”. In: Annual Review of Condensed Matter Physics 11.1.
- He, Kaiming et al. (2015). “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification”. In: Proceedings of the IEEE international conference on computer vision, pp. 1026–1034.
- Kardar, Mehran (2007). Statistical physics of fields. Cambridge University Press.
- Schoenholz, Samuel S et al. (2016). “Deep information propagation”. In: arXiv preprint arXiv:1611.01232.
- Roberts, Daniel A, Sho Yaida, and Boris Hanin (2022). The Principles of Deep Learning Theory: An Effective Theory Approach to Understanding Neural Networks. Cambridge University Press.
- Lee, Jaehoon et al. (2017). “Deep neural networks as gaussian processes”. In: arXiv preprint arXiv:1711.00165.